WTF Is Reactivity !?

Publié sur dev.to et medium.com

Les modèles de réactivité expliqués.

Préambule

Cela fait (déjà) 10 ans que je développe des applications et sites Web, pour autant l'écosystème JavaScript n'a jamais été aussi captivant qu'aujourd'hui !

En 2022, la communauté avait les yeux rivés sur le concept de "Signal" à tel point que la plupart des frameworks JavaScript l'ont implémenté dans leur moteur respectif. Je pense notamment à Preact qui propose des variables réactives détachées du cycle de vie des composants depuis Septembre 2022 ; ou plus récemment Angular, qui implémente les Signals de manière expérimentale en Mai 2023, puis officiellement depuis la version 18. D'autres librairies JavaScript ont fait le choix de repenser leur mode de fonctionnement...

Entre 2023 et jusqu'à présent, je n'ai cessé d'utiliser les Signals dans de multiples projets. Sa simplicité d'implémentation et d'utilisation m'a clairement convaincu, au point d'évoquer ses bienfaits à mon entourage professionnel lors d'ateliers techniques, de sessions de formations et de conférences.

Mais plus récemment, je me suis demandé si ce concept était si "révolutionnaire" / s'il n'existe pas d'alternatives aux Signals ? J'ai donc poursuivi cette réflexion et découvert qu'il existe des fonctionnements différents aux systèmes réactifs.

Cet article est un tour d'horizon des différents modèles de réactivité, ainsi que ma compréhension de leur mode de fonctionnement.

NB : À ce stade-là, vous l'aurez compris, je n'évoquerais pas les "Reactive Streams" de Java ; sinon j'aurais intitulé l'article "WTF Is Backpressure !?" 😉

Théorie

Lorsqu'on parle de modèles de réactivité, on parle avant toute chose de "programmation réactive", mais surtout de "réactivité".

La programmation réactive est un paradigme de développement qui permet de propager automatiquement le changement d'une source de données aux consommateurs.

On peut donc définir la réactivité comme étant la capacité à mettre à jour des dépendances en temps réel, en fonction du changement de données.

NB : En clair, lorsqu'un utilisateur remplit/soumet un formulaire, on se doit de réagir à ces changements, afficher un composant de chargement, ou autre chose qui indique qu'il se passe quelque chose... Autre exemple, à la réception de données de manière asynchrone, on se doit de réagir en affichant tout ou partie de ces données, exécuter une nouvelle action, etc...

Dans ce contexte, les librairies réactives nous fournissent des variables qui se mettent à jour automatiquement et qui se propagent efficacement, facilitant l'écriture de code simple et performant.

Pour être efficace, ces systèmes doivent re-calculer/re-évaluer ces variables, si et seulement si, leurs valeurs ont changé ! De même, pour que les données diffusées restent cohérentes et à jour, le système ne doit pas afficher d'état intermédiaire (notamment lors des phases de calcul du changement d'état).

NB : L'état fait référence aux données/valeurs utilisées tout au long de la durée de vie d'un programme / d'une application.

Okay, mais alors... Quels sont ces fameux "modèles de réactivité" !?

PUSH, ou Réactivité "Immédiate"

Le premier modèle de réactivité se prénomme "PUSH" (aussi appelé réactivité "immédiate"). Ce système repose sur les principes suivants :

• Initialisation de sources de données (communément appelées "Observables")
• Les composants / fonctions s'abonnent à ces sources de données (ce sont les consommateurs)
• Les données se propagent immédiatement aux consommateurs (communément appelés "Observers") lorsqu'une valeur change

Vous l'aurez compris, le modèle "PUSH" repose sur le design pattern "Observable/Observer".

1er Cas d'Usage : État Initial et Changement d'État

Admettons l'état initial suivant,

let a = { firstName: 'John', lastName: 'Doe' };
const b = a.firstName;
const c = a.lastName;
const d = `${b} ${c}`;

Depuis une librairie réactive (telle que RxJS), cet état initial ressemblerait plutôt à ceci :

let a = observable.of({ firstName: 'John', lastName: 'Doe' });
const b = a.pipe(map(a => a.firstName));
const c = a.pipe(map(a => a.lastName));
const d = merge(b, c).pipe(reduce((b, c) => `${b} ${c}`));

NB : Pour les bienfaits de cet article, toutes les portions de code sont à considérer comme étant du "pseudo-code".

Supposons maintenant qu'un consommateur (un composant, par exemple) souhaite logger la valeur de l'état D lorsque cette source de données est mise à jour,

d.subscribe(value => console.log(value));

Notre composant s'abonne donc au flux de données ; il reste encore à déclencher un changement,

a.next({ firstName: 'Jane', lastName: 'Doe' });

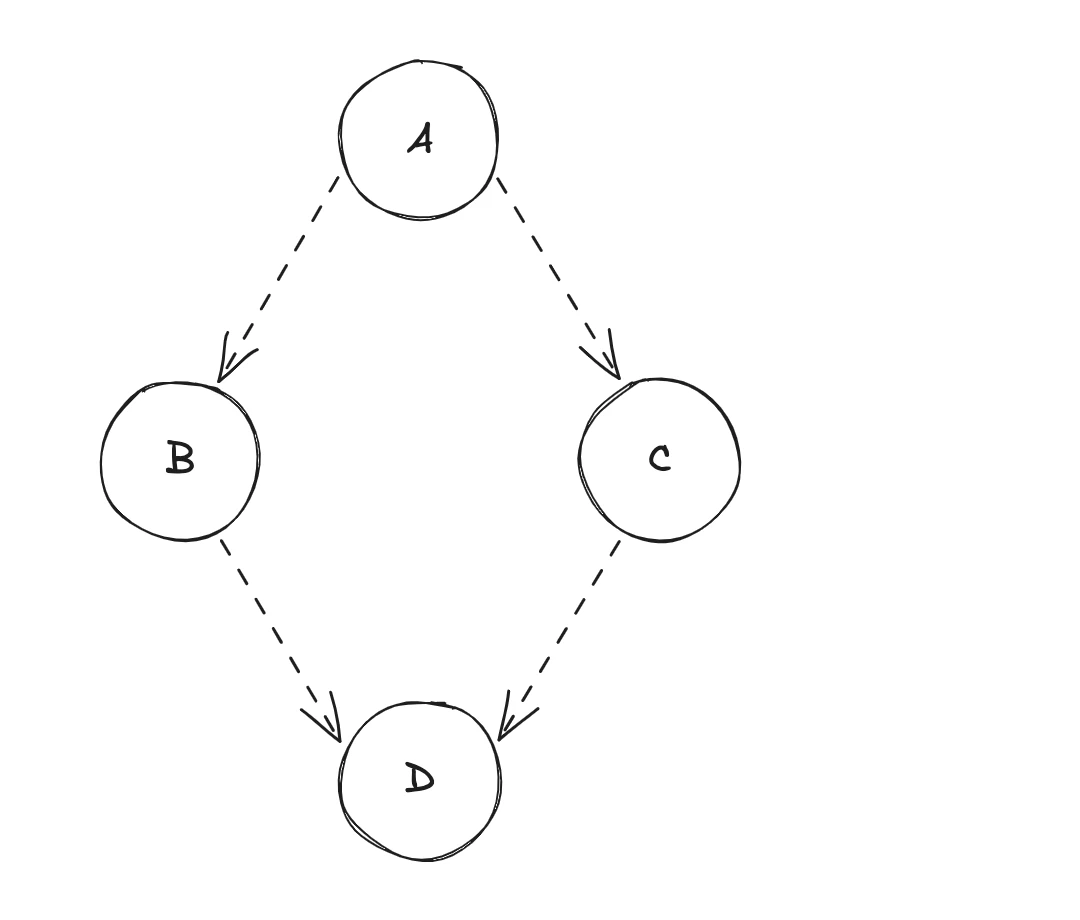
À partir de là, le système "PUSH" perçoit le changement et le diffuse automatiquement aux consommateurs. D'après l'état initial ci-dessus, voici une description des opérations pouvant se produire :

• Changement d'état de la source de données A !
• Diffusion de la valeur de A vers B (calcul de la source de données B) ;
• Puis, diffusion de la valeur de B vers D (calcul de la source de données D) ;
• Diffusion de la valeur de A vers C (calcul de la source de données C) ;
• Enfin, diffusion de la valeur C vers D (re-calcul de la source de données D) ;

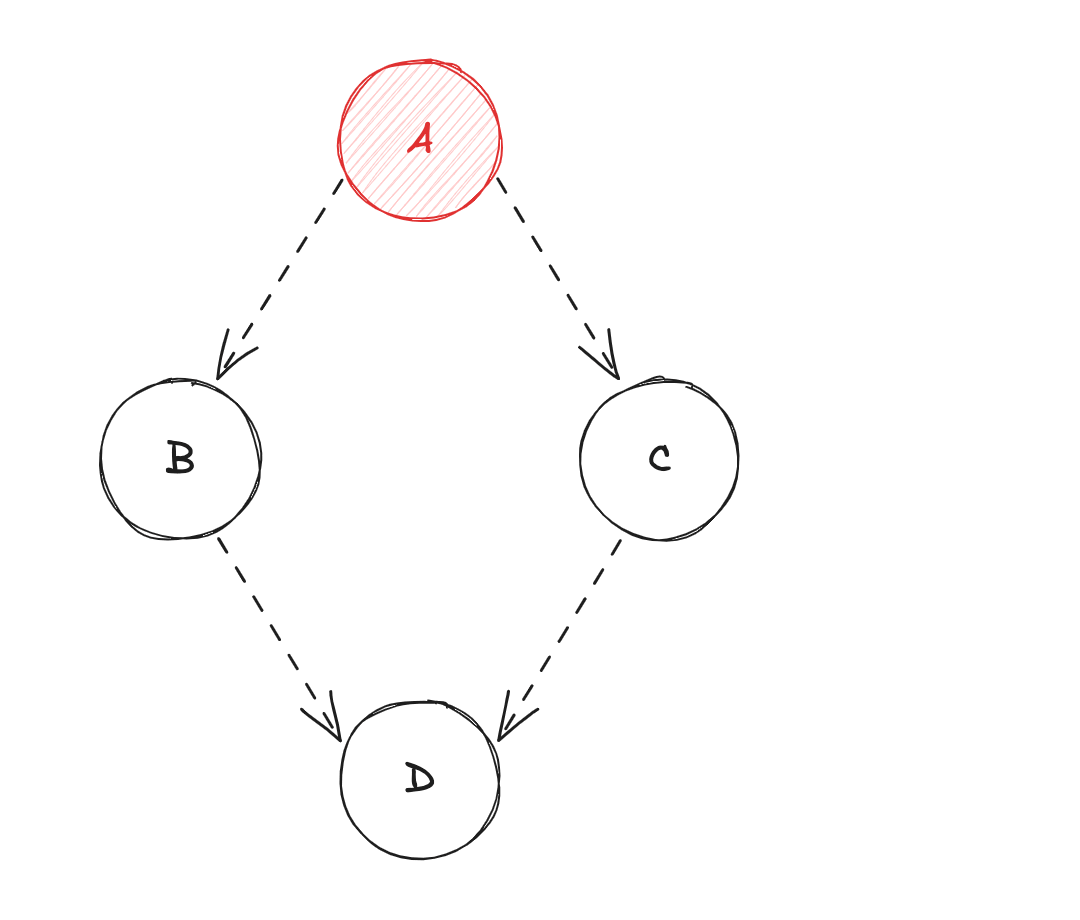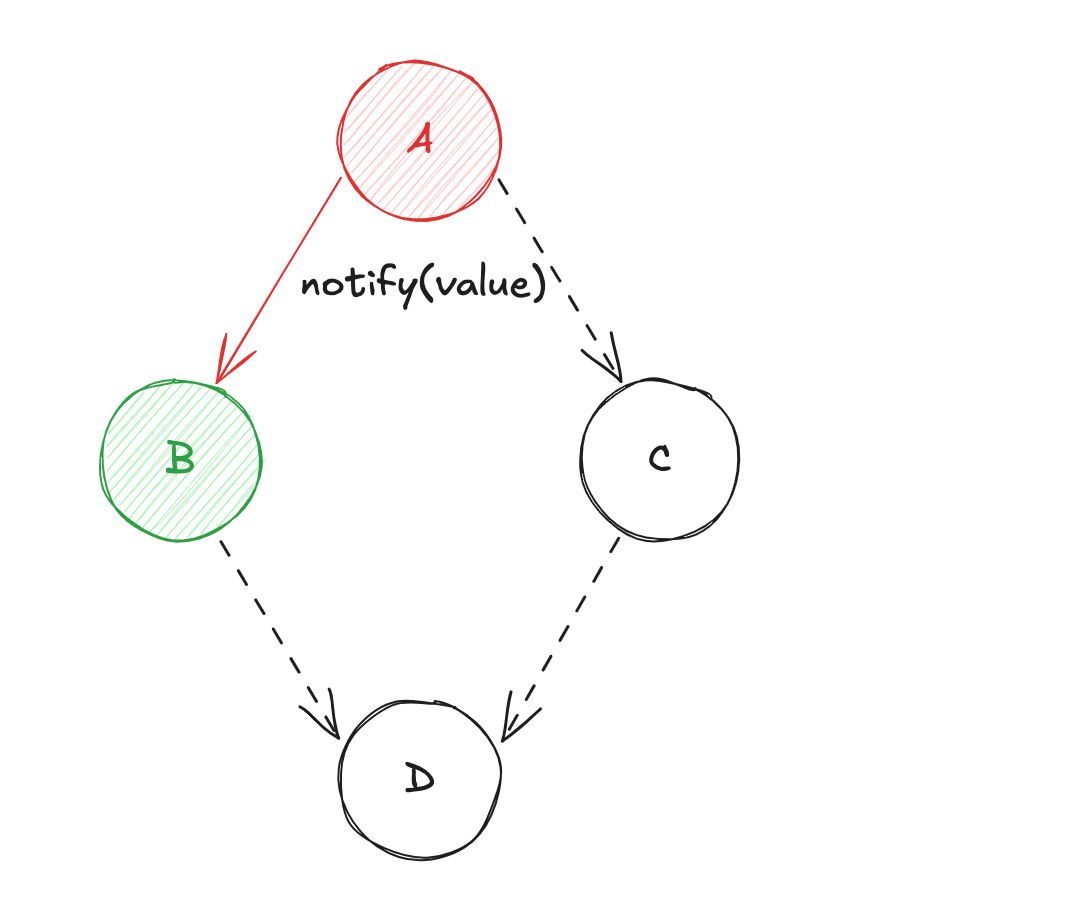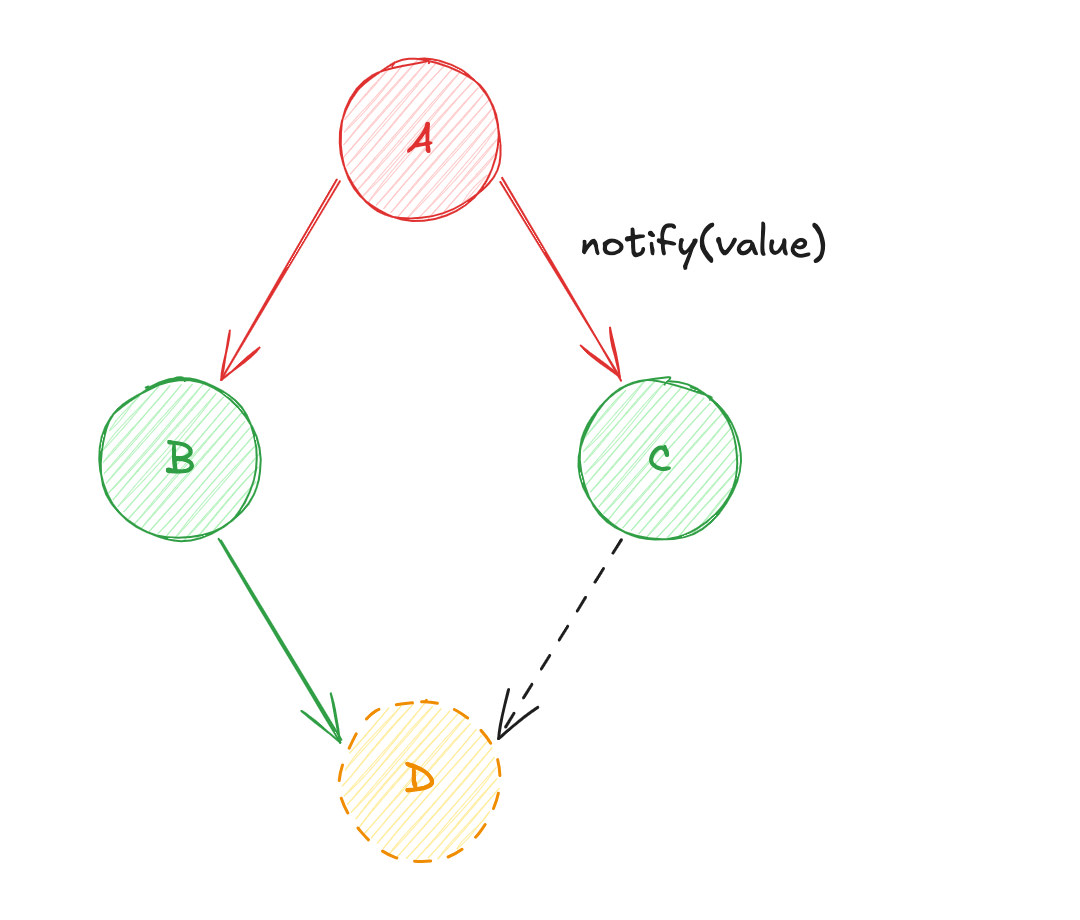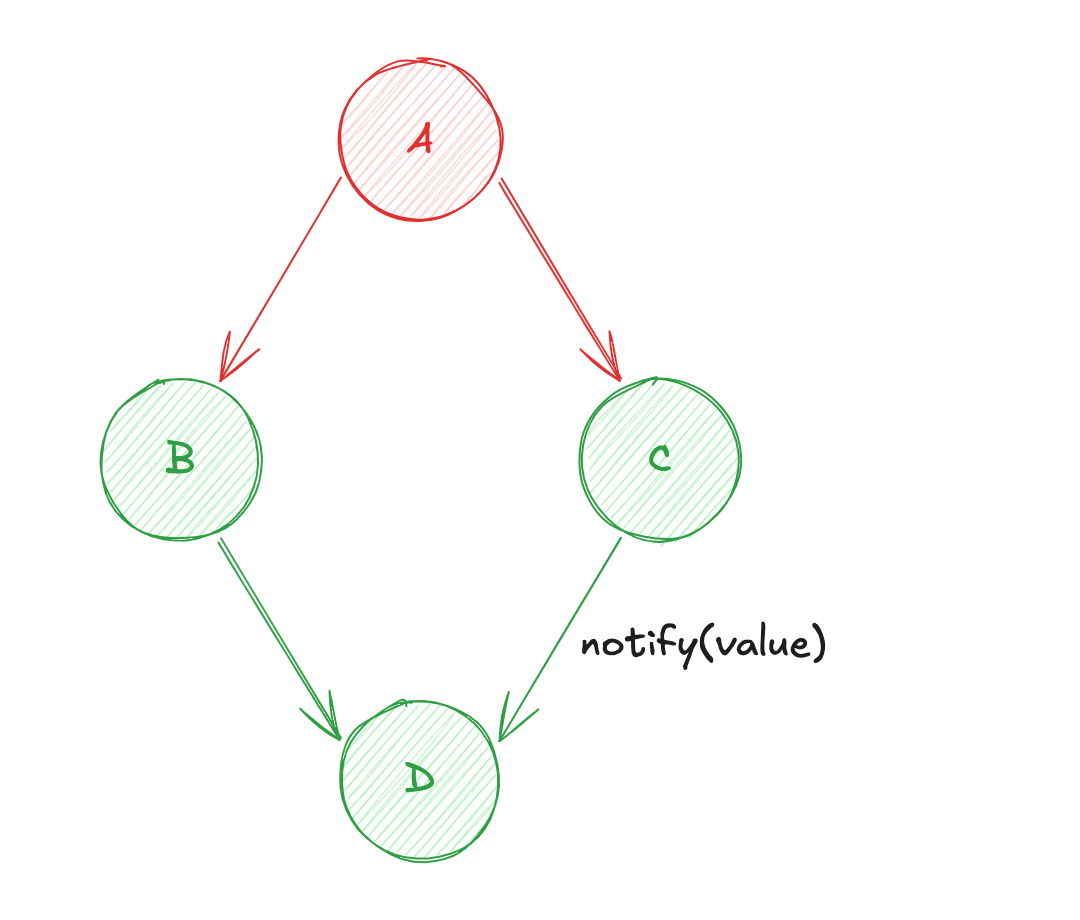
Une des problématiques de ce système repose sur l'ordre de calcul. En effet, d'après notre cas d'usage, vous remarquerez que D est susceptible d'être évalué deux fois : une première fois avec la valeur de C à son état précédent ; et une seconde fois avec la valeur de C à jour ! Dans ce genre de modèle de réactivité, cette difficulté se nomme le "Diamond Problem" ♦️

2ème Cas d'Usage : Prochaine Itération

Admettons maintenant que l'état repose sur deux sources de données principales,

let a = observable.of({ firstName: 'Jane', lastName: 'Doe' });
let e = observable.of('');
const b = a.pipe(map(a => a.firstName));
const c = merge(a, e).pipe(reduce((a, e) => `${e} ${a.lastName}`));
const d = merge(b, c).pipe(reduce((b, c) => `${b} ${c}`));

d.subscribe(value => console.log(value));
e.next('Phoenix');

Lors de la mise à jour de E, le système va re-calculer l'entièreté de l'état, ce qui lui permet de conserver une source de vérité en écrasant l'état précédent.

• Changement d'état de la source de données E !
• Diffusion de la valeur de A vers B (calcul de la source de données B) ;
• Puis, diffusion de la valeur de B vers D (calcul de la source de données D) ;
• Diffusion de la valeur de A vers C (calcul de la source de données C) ;
• Diffusion de la valeur de E vers C (re-calcul de la source de données C) ;
• Enfin, diffusion de la valeur C vers D (re-calcul de la source de données D) ;

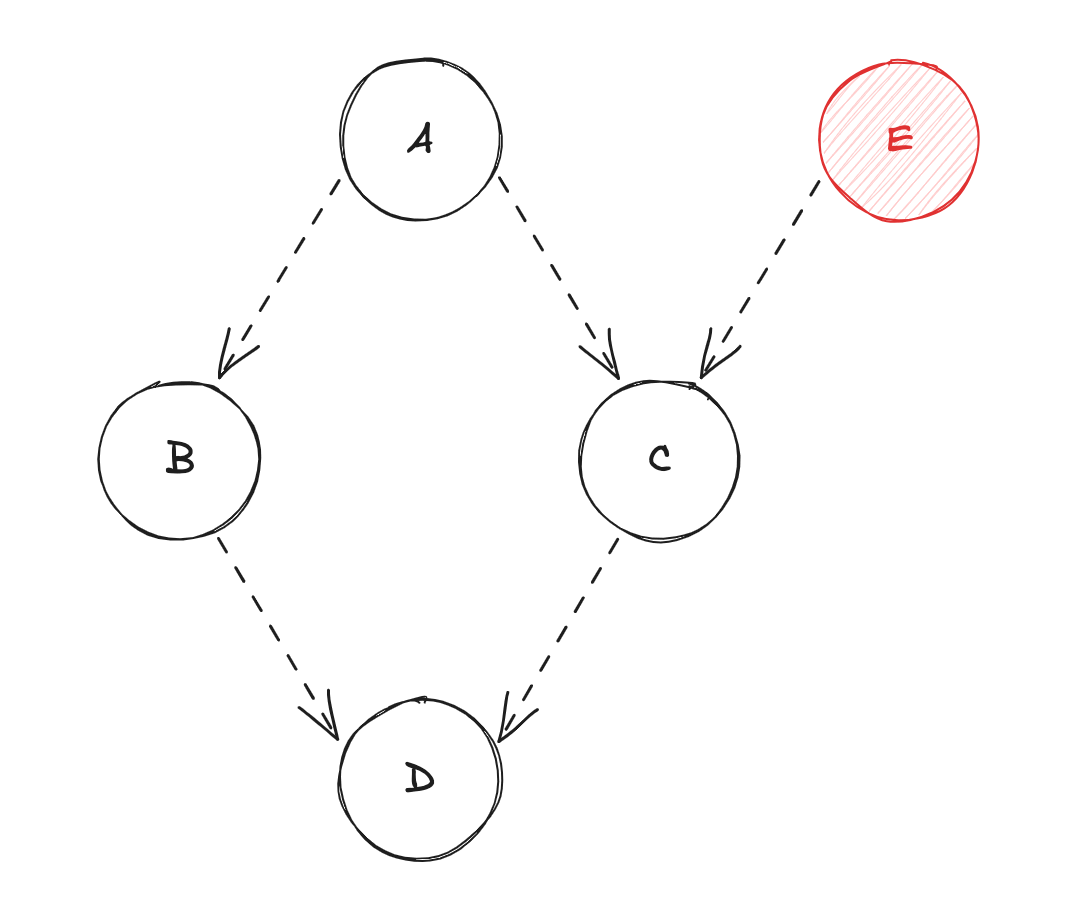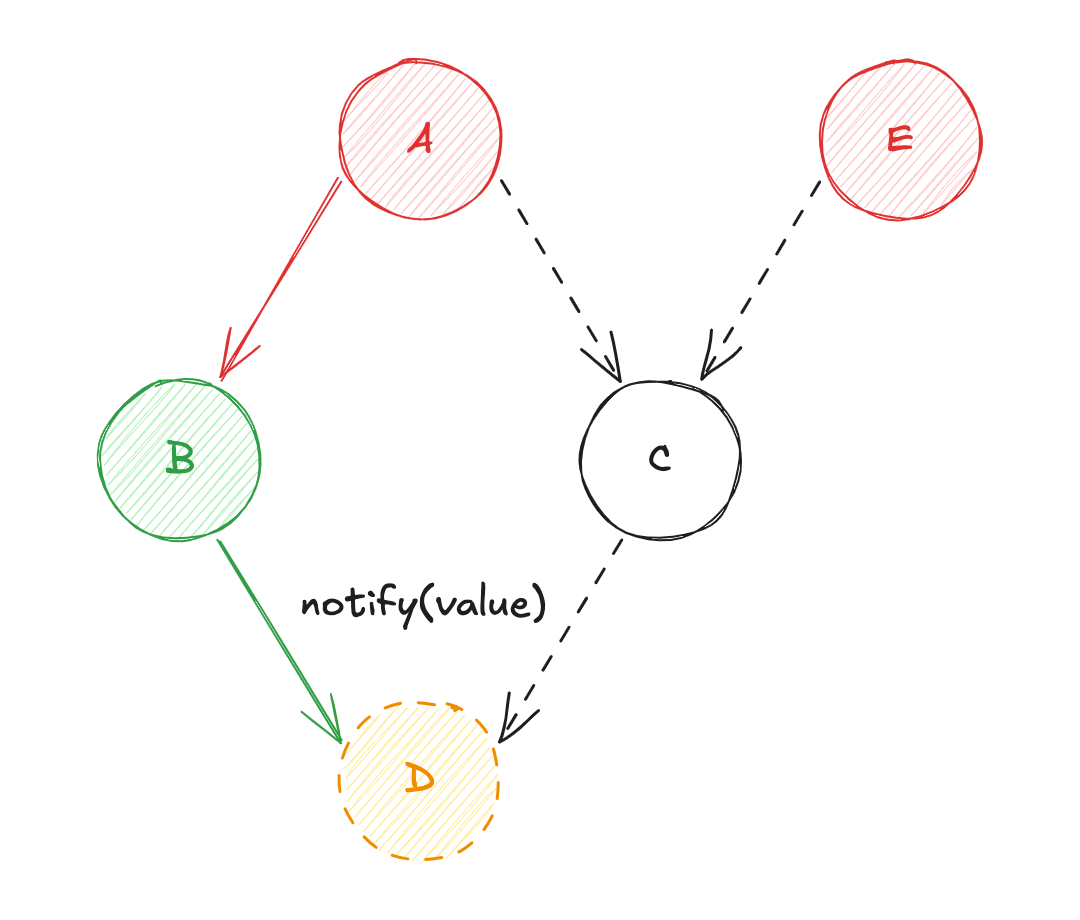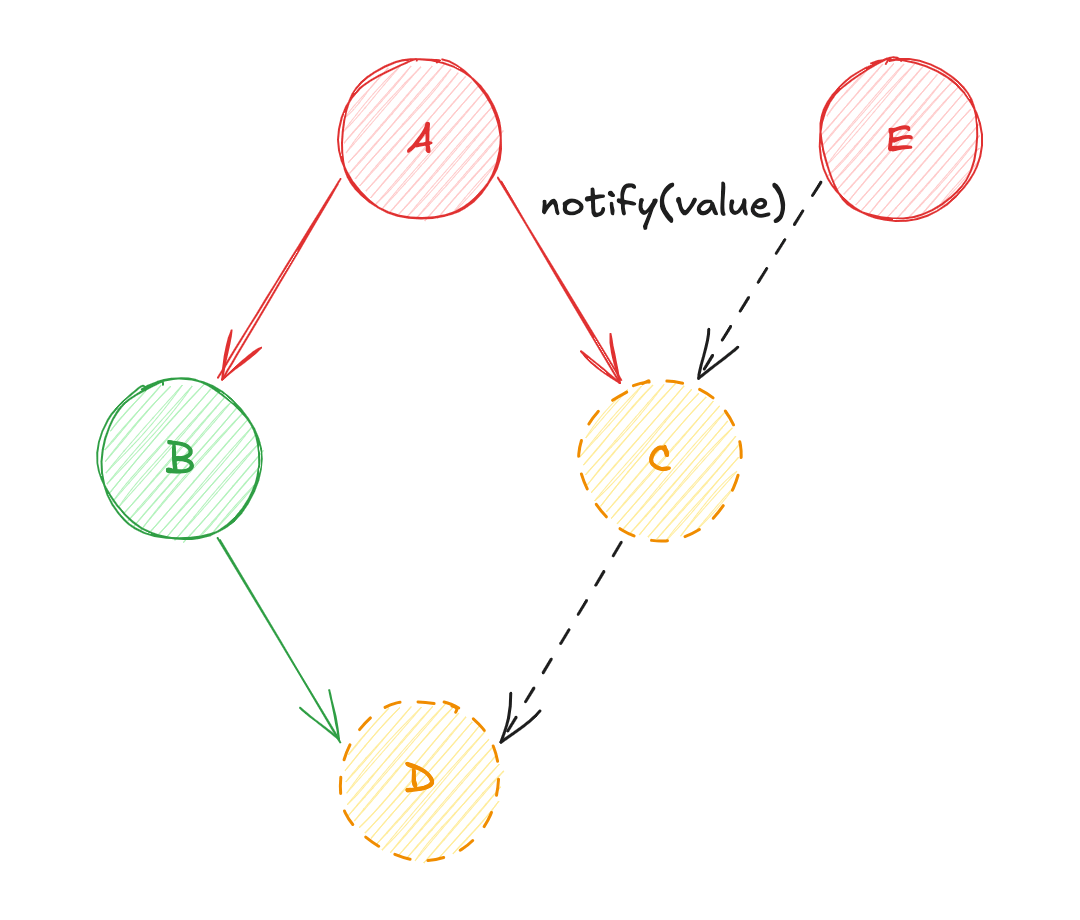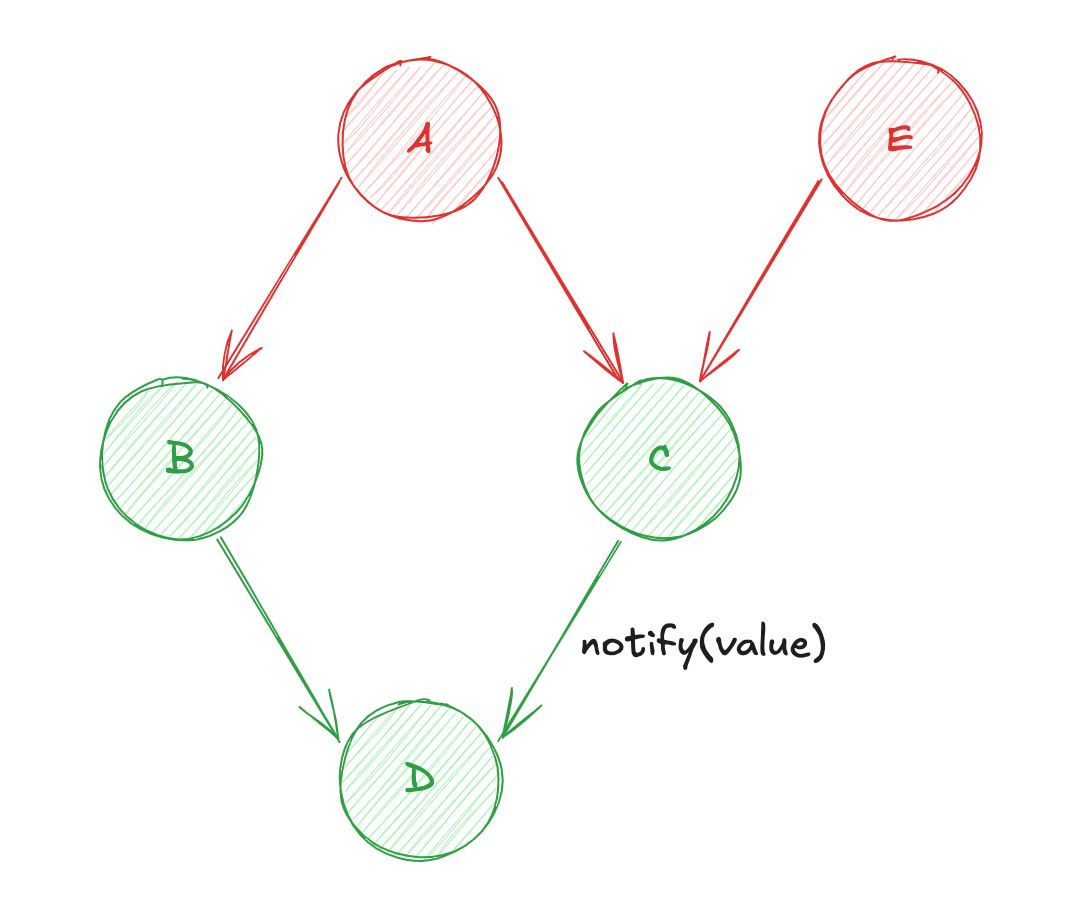
À nouveau, le "Diamond Problem" survient... Cette fois-ci sur la source de données C qui est potentiellement évaluée 2 fois, et toujours sur D.

Diamond Problem

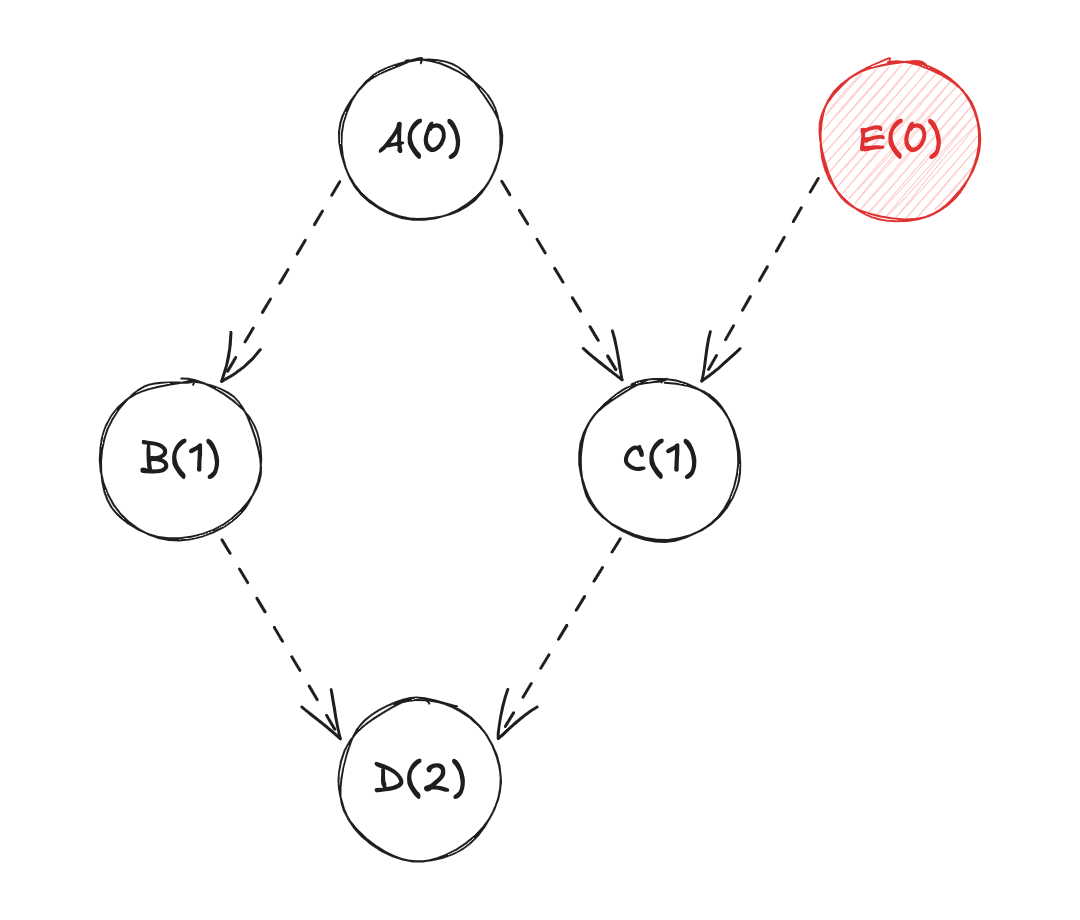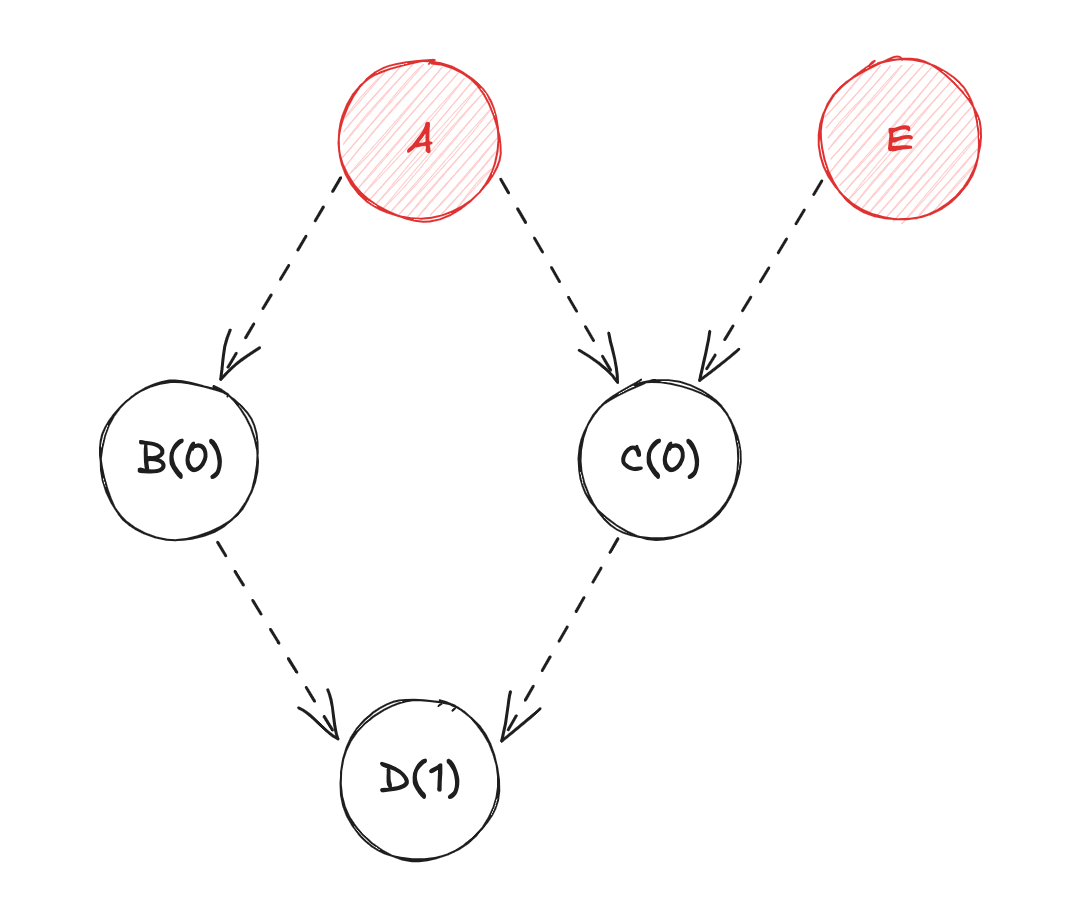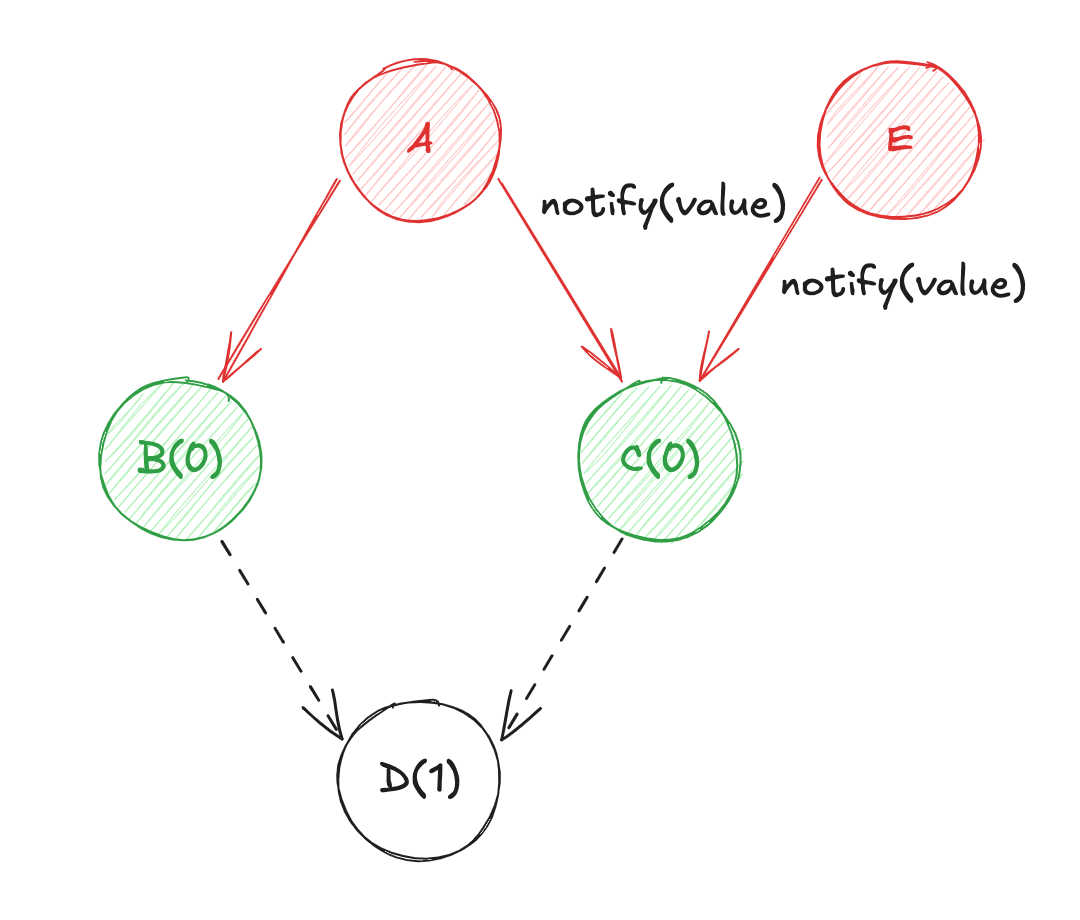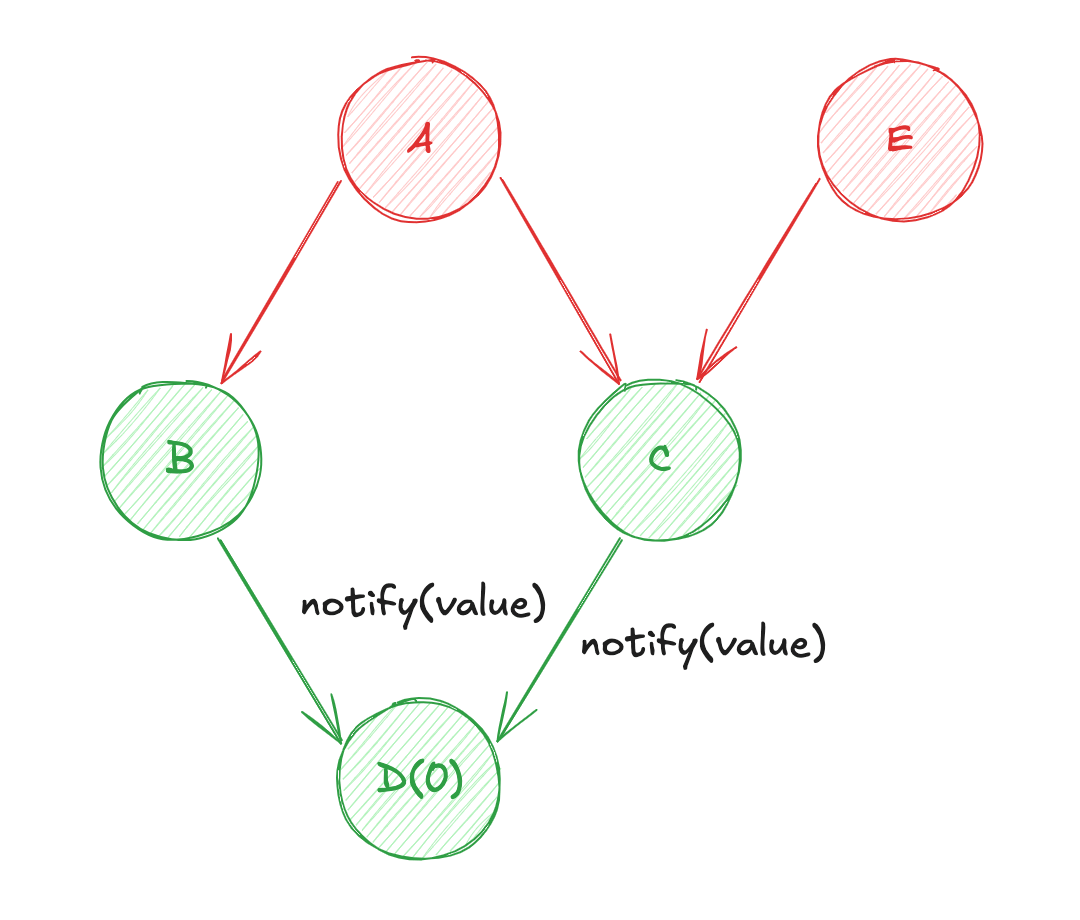
Le "Diamond Problem" n'est pas un nouveau défi dans le modèle réactif "immédiat". Certains algorithmes de calcul (notamment ceux de MobX) permettent de versionner "les nœuds de l'arbre des dépendances réactives" afin de niveler le calcul de l'état. Avec ce mode de fonctionnement, le système évaluerait d'abord les sources de données "racine" (A et E dans notre exemple), puis B et C, enfin D. Le changement d'ordre des calculs de l'état permet de corriger ce type de problème.

PULL, ou Réactivité "Paresseuse"

Le deuxième modèle de réactivité s'intitule "PULL". Contrairement au modèle "PUSH", celui-ci repose sur les principes suivants :

• Déclaration de variables réactives
• Le système diffère le calcul de l'état
• L'état dérivé est calculé en fonction de ses dépendances
• Le système évite les mises à jour excessives

C'est bien cette dernière règle qu'il faut retenir : contrairement au système précédent, ce dernier diffère le calcul de l'état afin de minimiser les évaluations multiples d'une même source de données.

1er Cas d'Usage : État Initial et Changement d'État

Conservons l'état initial précédent...

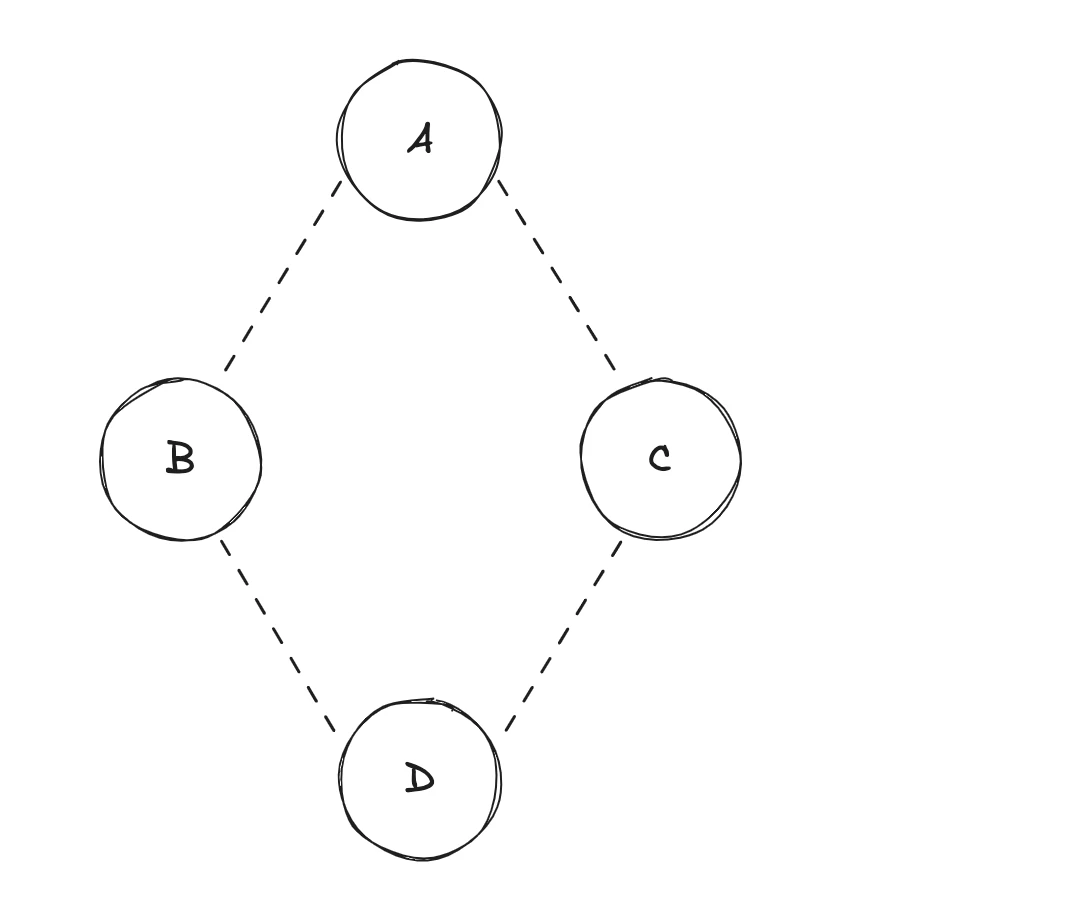
Dans ce type de système, la syntaxe de l'état initial se présenterait sous la forme suivante :

let [a, setA] = state({ firstName: 'John', lastName: 'Doe' });
const b = computed(() => a.firstName, [a]);
const c = computed(() => a.lastName, [a]);
const d = computed(() => `${b} ${c}`, [b, c]);

NB : Les adeptes de React reconnaîtront sûrement cette syntaxe 😎

La déclaration d'une variable réactive donne "naissance" à un tuple : variable immutable d'un côté ; fonction de mise à jour de cette variable de l'autre. Les déclarations restantes (B, C et D dans notre exemple) sont considérées comme des états dérivées puisqu'ils "écoutent" leurs dépendances respectives.

setA({ firstName: 'Jane', lastName: 'Doe' });

La particularité d'un système "paresseux" repose sur le fait qu'il ne propage pas instantanément le changement, mais seulement lorsque celui-ci n'est pas explicitement demandé.

effect(() => console.log(d), [d]);

Dans un modèle "PULL", l'utilisation d'un effect() (depuis un composant), pour logger la valeur d'une variable réactive (spécifiée depuis les dépendances), va exécuter le calcul du changement de l'état :

• D va vérifier si ses dépendances (B et C) ont été mises à jour ;
• B va vérifier si sa dépendance (A) a été mise à jour ;
• A va diffuser sa valeur à B (calcul de la valeur de B) ;
• C va vérifier si sa dépendance (A) a été mise à jour ;
• A va diffuser sa valeur à C (calcul de la valeur de C) ;
• B et C vont diffuser leur valeur respective à D (calcul de la valeur de D) ;

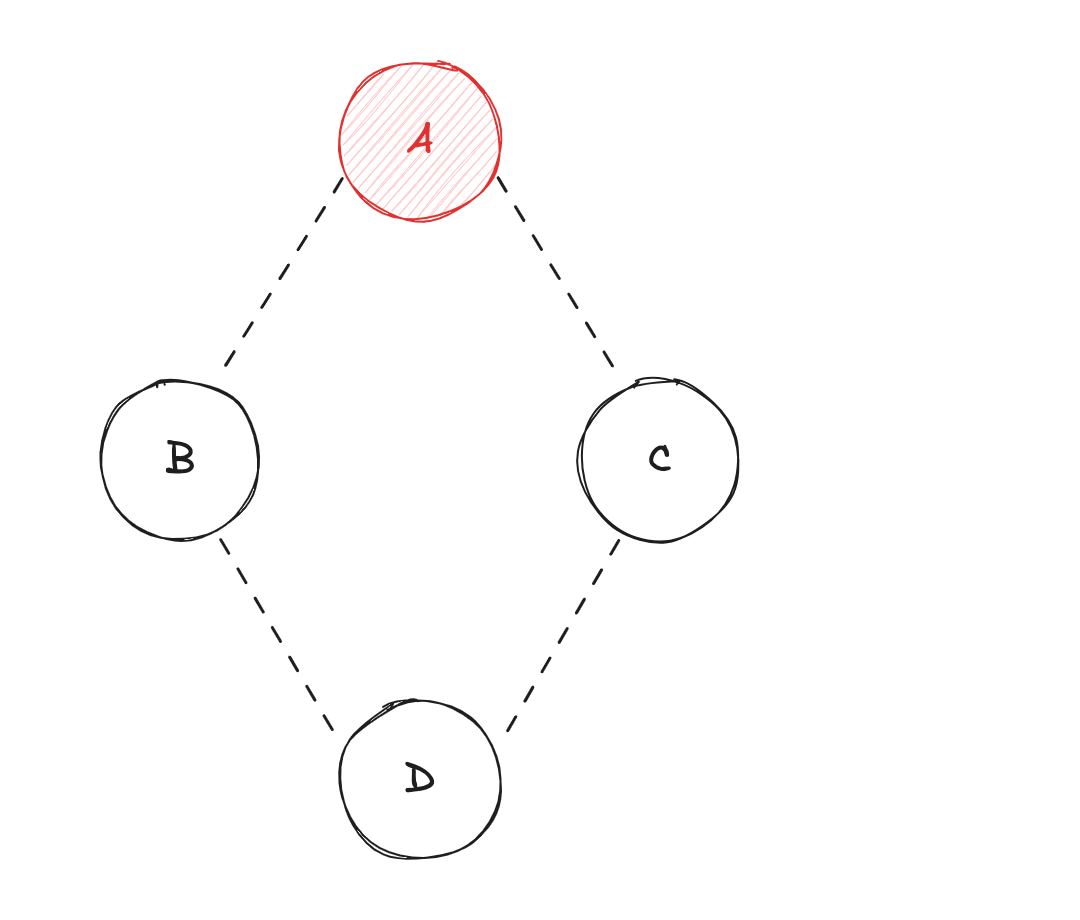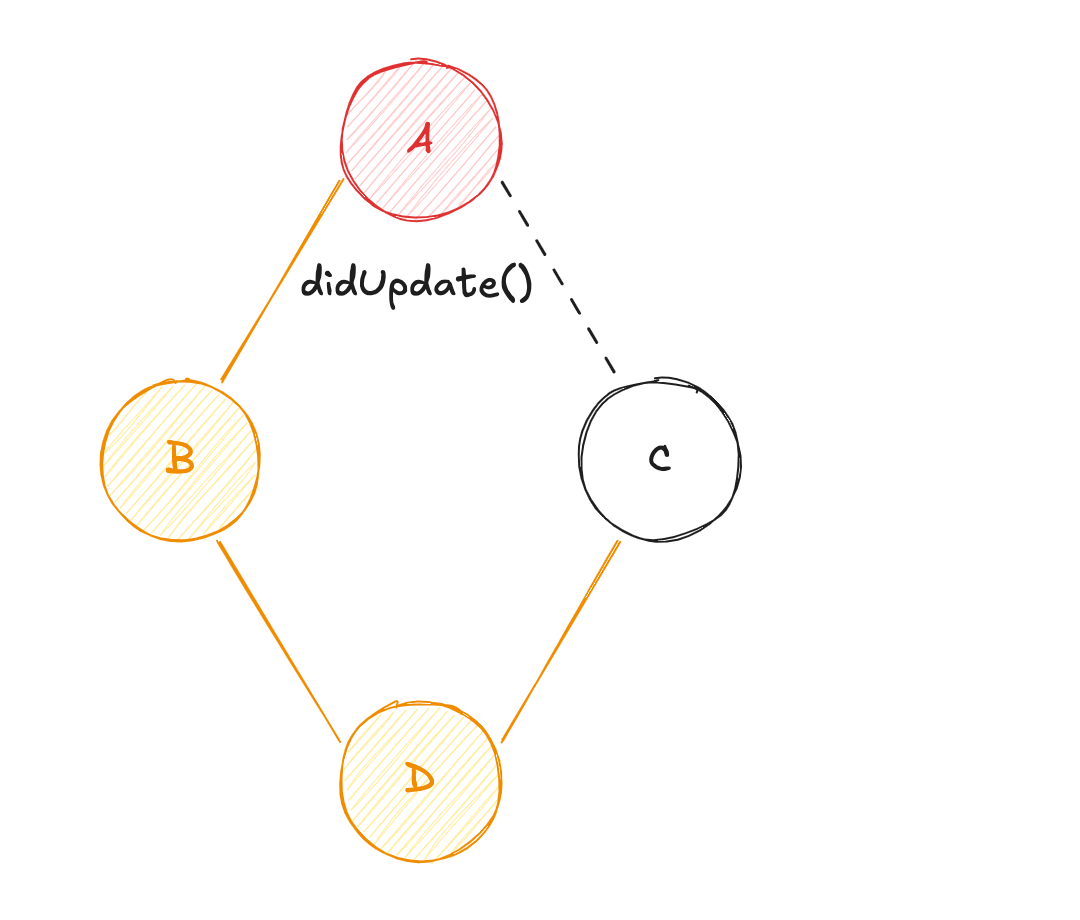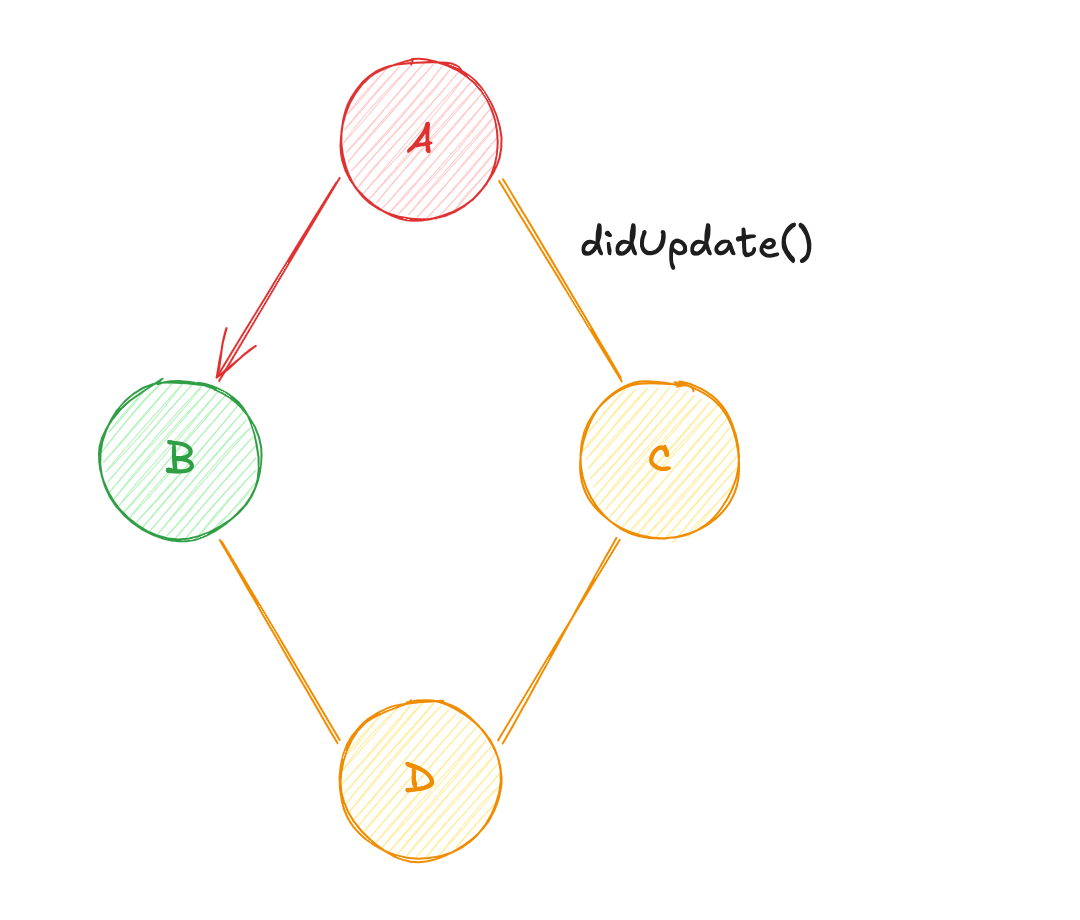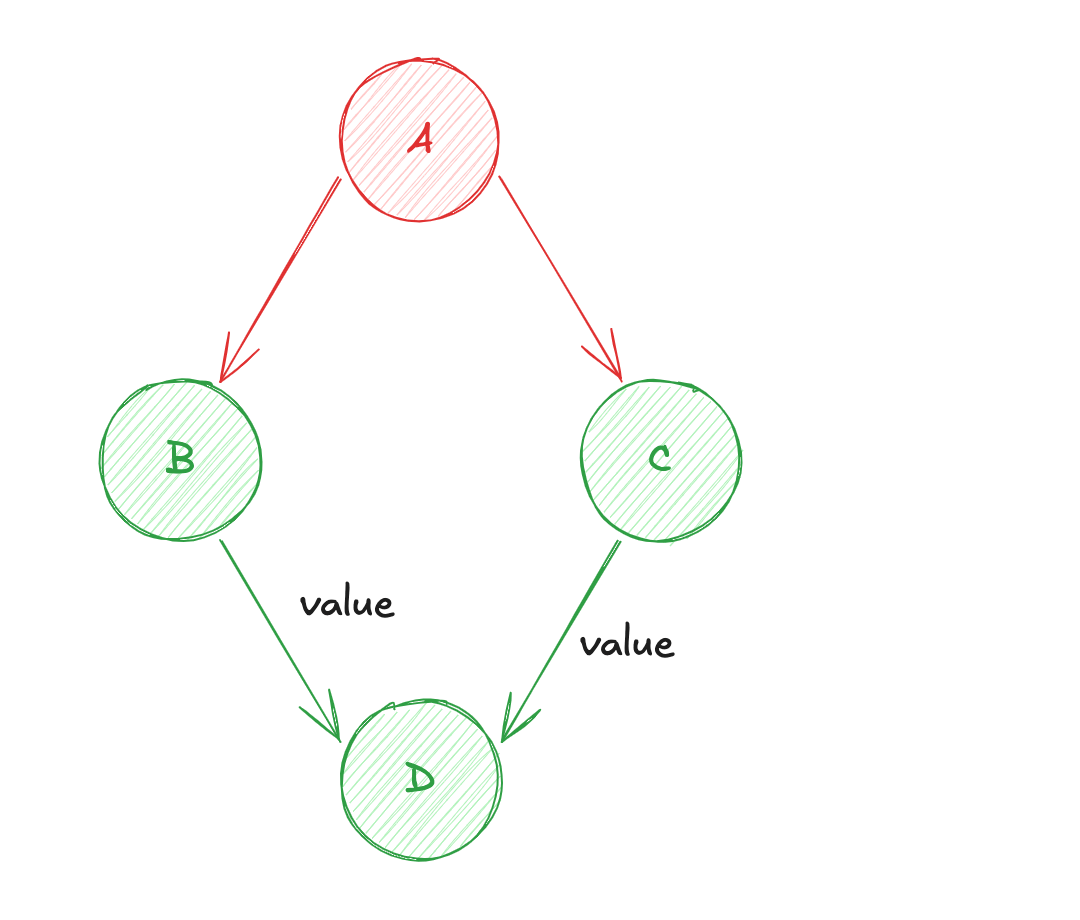
Une optimisation de ce système est possible lors de l'interrogation des dépendances. En effet, d'après la situation ci-dessus, A est interrogé deux fois pour savoir s'il a été mis à jour. Or la 1ère interrogation pourrait suffire à définir si l'état a été mis à jour. C n'aurait pas besoin d'effectuer cette action... A pourrait seulement diffuser sa valeur.

2ème Cas d'Usage : Prochaine Itération

Complexifions quelque peu l'état en ajoutant une deuxième variable réactive "racine",

let [a, setA] = state({ firstName: 'Jane', lastName: 'Doe' });
let [e, setE] = state('');
const b = computed(() => a.firstName, [a]);
const c = computed(() => `${e} ${a.lastName}`, [a, e]);
const d = computed(() => `${b} ${c}`, [b, c]);

effect(() => console.log(d), [d]);
setE('Phoenix');

Encore une fois, le système va différer le calcul de l'état tant qu'il n'est pas explicitement demandé. En conservant l'effect précédant, la mise à jour d'une nouvelle variable réactive va entraîner les étapes suivantes :

• D va vérifier si ses dépendances (B et C) ont été mises à jour ;
• B va vérifier si sa dépendance (A) a été mise à jour ;
• C va vérifier si ses dépendances (A et E) ont été mises à jour ;
• E va diffuser sa valeur à C, et C va récupérer la valeur de A par mémoïsation (re-calcul de la valeur de C) ;
• C va diffuser sa valeur à D, et D va récupérer la valeur de B par mémoïsation (re-calcul de la valeur de D) ;

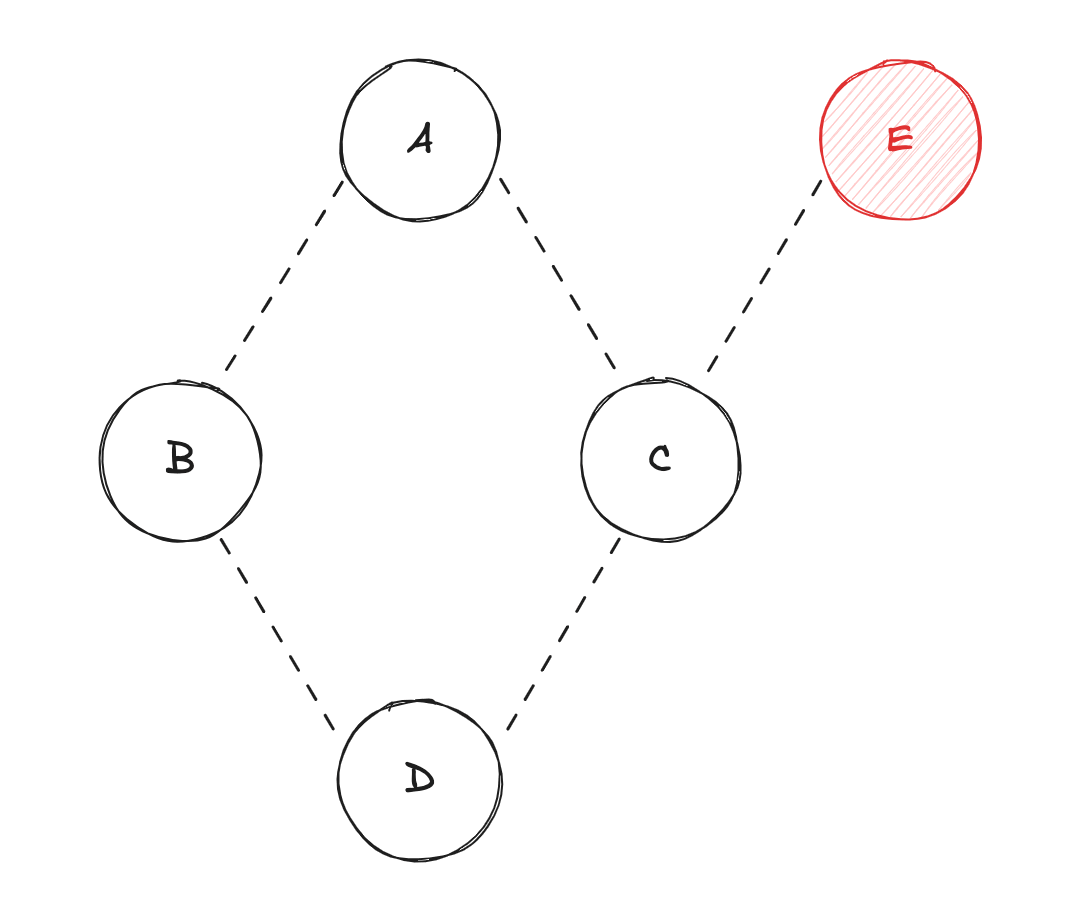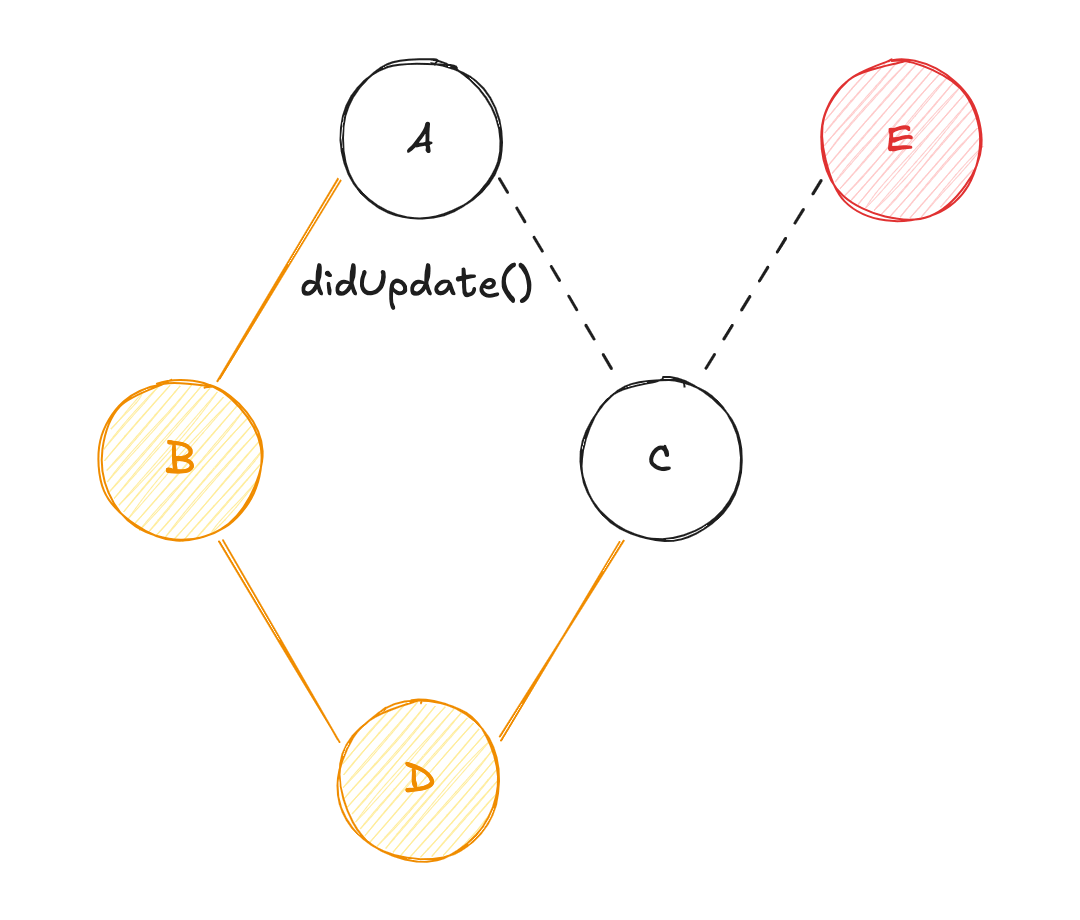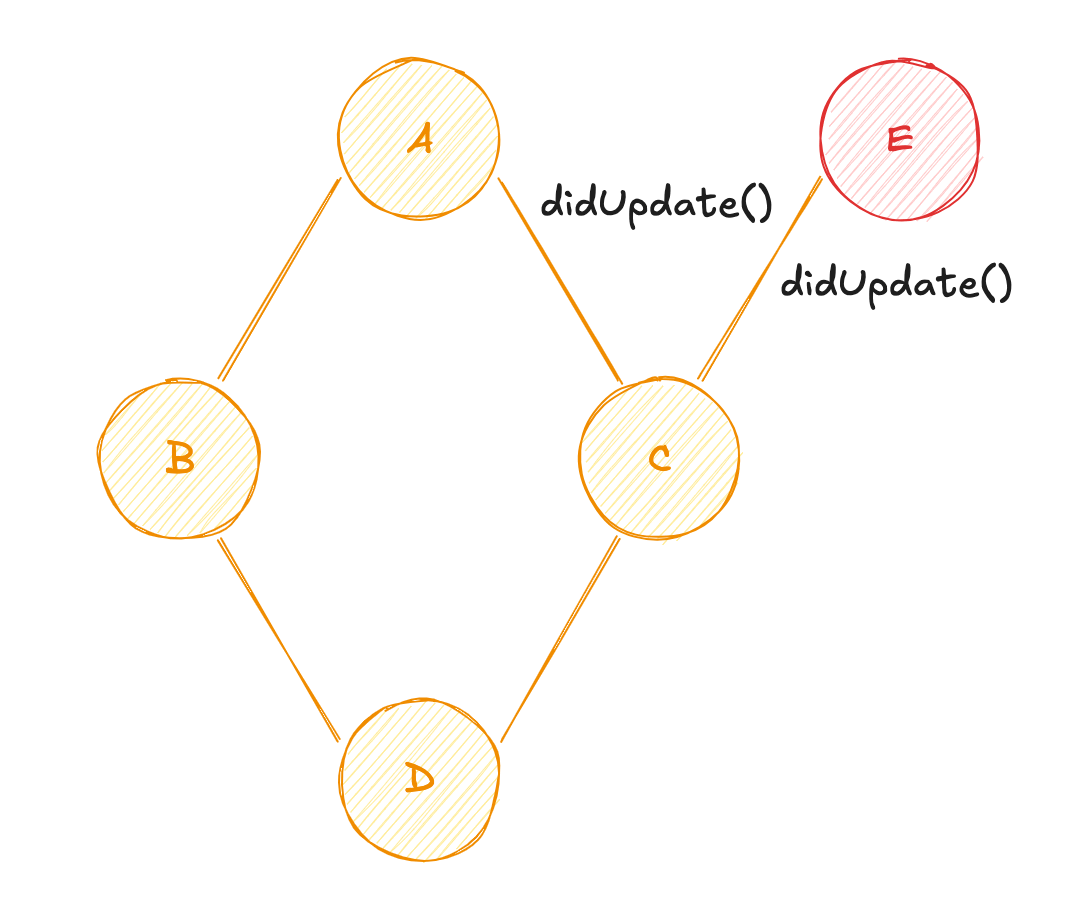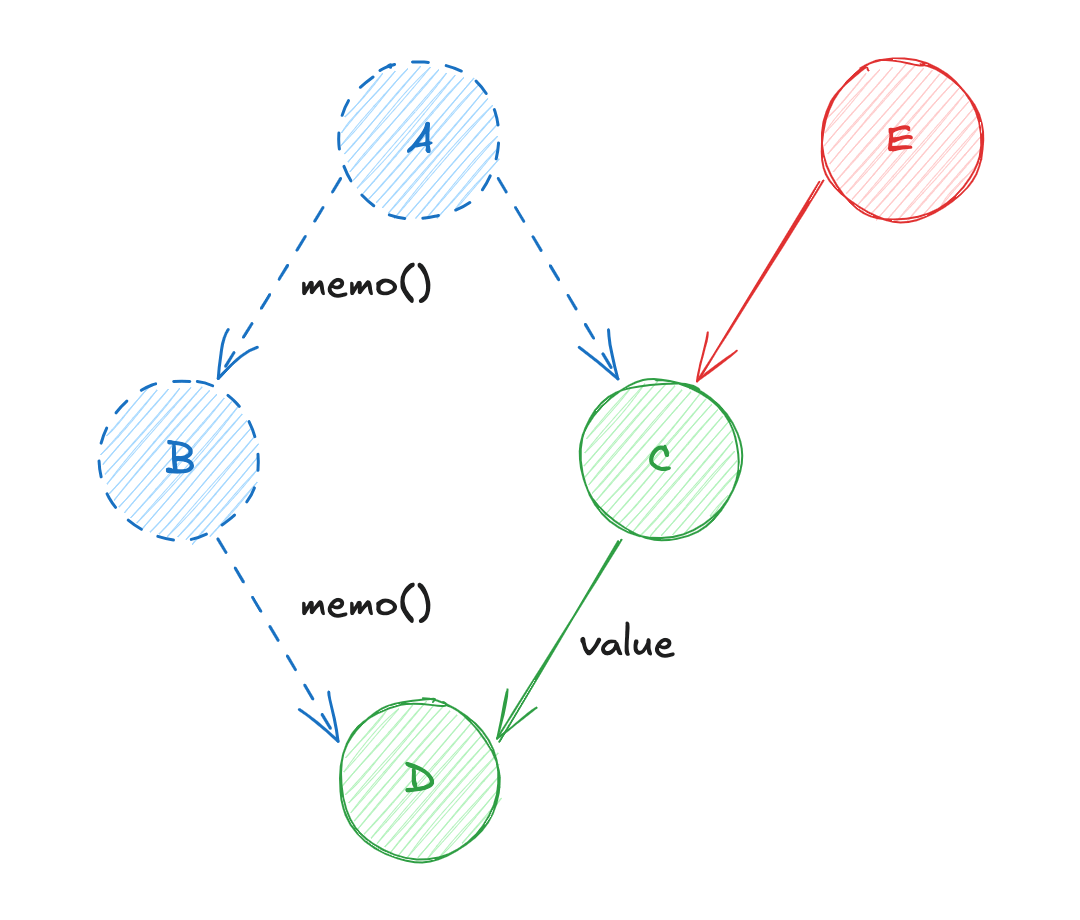
Puisque la valeur de A n'a pas changé, le calcul de cette variable n'est pas nécessaire (même chose pour la valeur de B). Dans ce cas-là, l'utilisation d'algorithmes de mémoïsation permet de gagner en performance lors du calcul de l'état.

PUSH-PULL, et Réactivité "Granulaire"

Le dernier modèle de réactivité est le système "PUSH-PULL". La mention "PUSH" reflète le fait que la notification du changement est propagée immédiatement, et la notion de "PULL" réfère à la récupération des valeurs de l'état à la demande. Ce mode de fonctionnement est étroitement lié à ce qu'on appelle la réactivité "granulaire" qui réagit aux règles suivantes :

• Déclaration de variables réactives (on parle de primitives réactives)
• Les dépendances sont suivies de manière atomique
• La propagation du changement est ciblée

À noter que ce type de réactivité n'est pas exclusif au modèle "PUSH-PULL". La réactivité "granulaire" est le fait que les dépendances du système soient suivies finement. Il existe donc des modèles de réactivité PUSH et PULL qui fonctionnent également de la sorte (je pense notamment à Jotai ou encore à Recoil).

1er Cas d'Usage : État Initial et Changement d'État

Toujours d'après l'état initial précédent... La déclaration d'un état initial dans un système à réactivité "granulaire" ressemblerait à ceci :

let a = signal({ firstName: 'John', lastName: 'Doe' });
const b = computed(() => a.value.firstName);
const c = computed(() => a.value.lastName);
const d = computed(() => `${b.value} ${c.value}`);

NB : L'utilisation du mot clé signal n'est pas qu'anecdotique ici 😉

En termes de syntaxe, on est très proche du modèle "PUSH", pour autant il y a une différence notable importante : les dépendances ! Dans un système à réactivité "granulaire", il n'est pas nécessaire de déclarer explicitement les dépendances requises pour le calcul d'un état dérivé, car ces états suivent implicitement les variables qu'ils utilisent. Dans notre cas, B et C vont suivre automatiquement le changement de valeur de A, et D va suivre le changement de B et C.

a.value = { firstName: 'Jane', lastName: 'Doe' };

Dans ce genre système, la mise à jour d'une variable réactive est plus efficace que dans un simple modèle "PUSH", puisque le changement est automatiquement propagé aux variables dérivées qui en dépendent (seulement la notification, pas la valeur).

effect(() => console.log(d.value));

Ensuite, à la demande (reprenons l'exemple du logger), l'utilisation de D au sein du système va permettre de récupérer les valeurs des états racines associés (dans notre cas A), puis de calculer les valeurs des états dérivés (B et C), pour enfin évaluer D. Plutôt intuitif comme mode de fonctionnement !

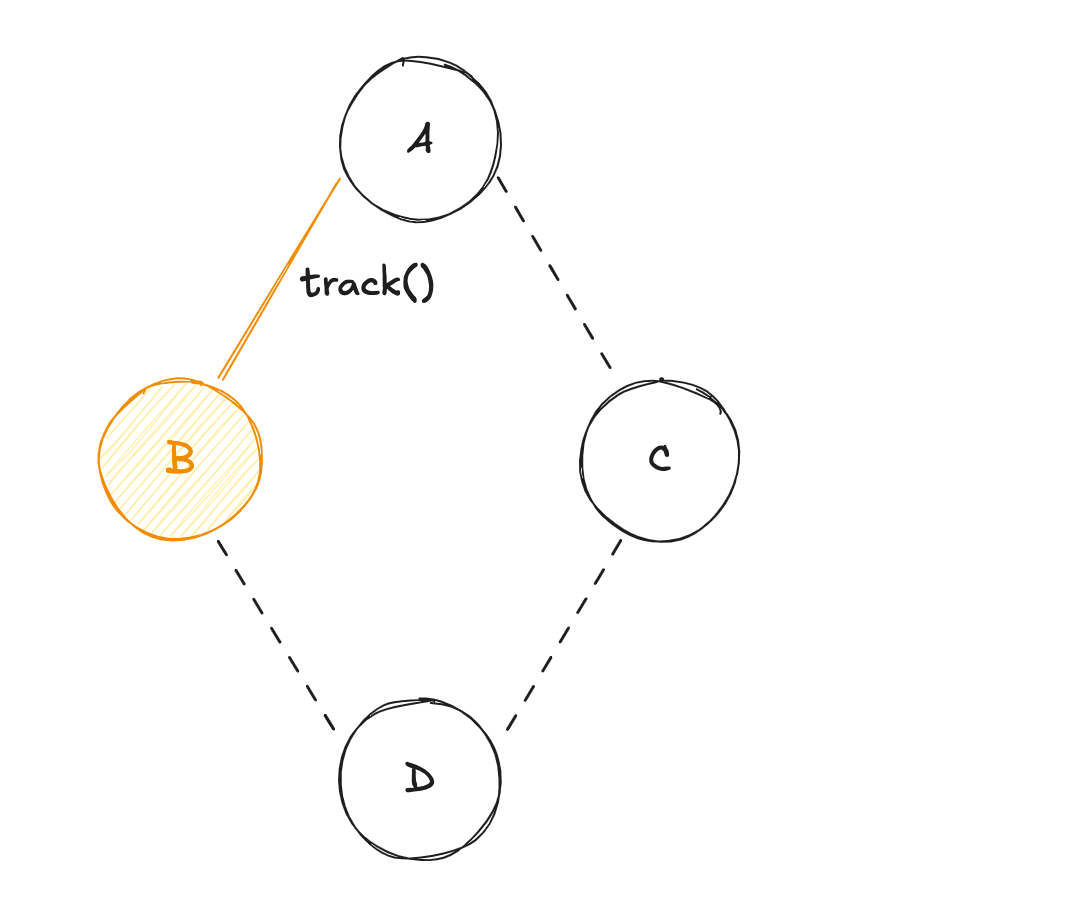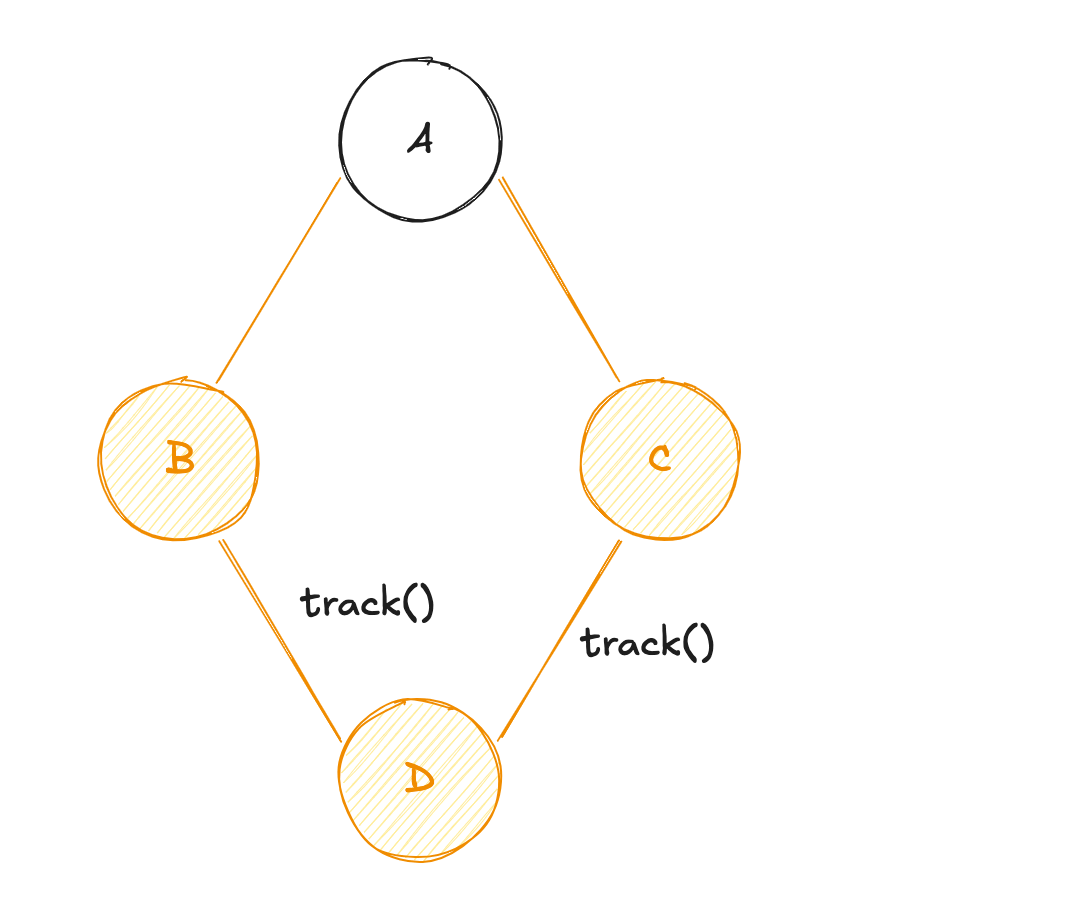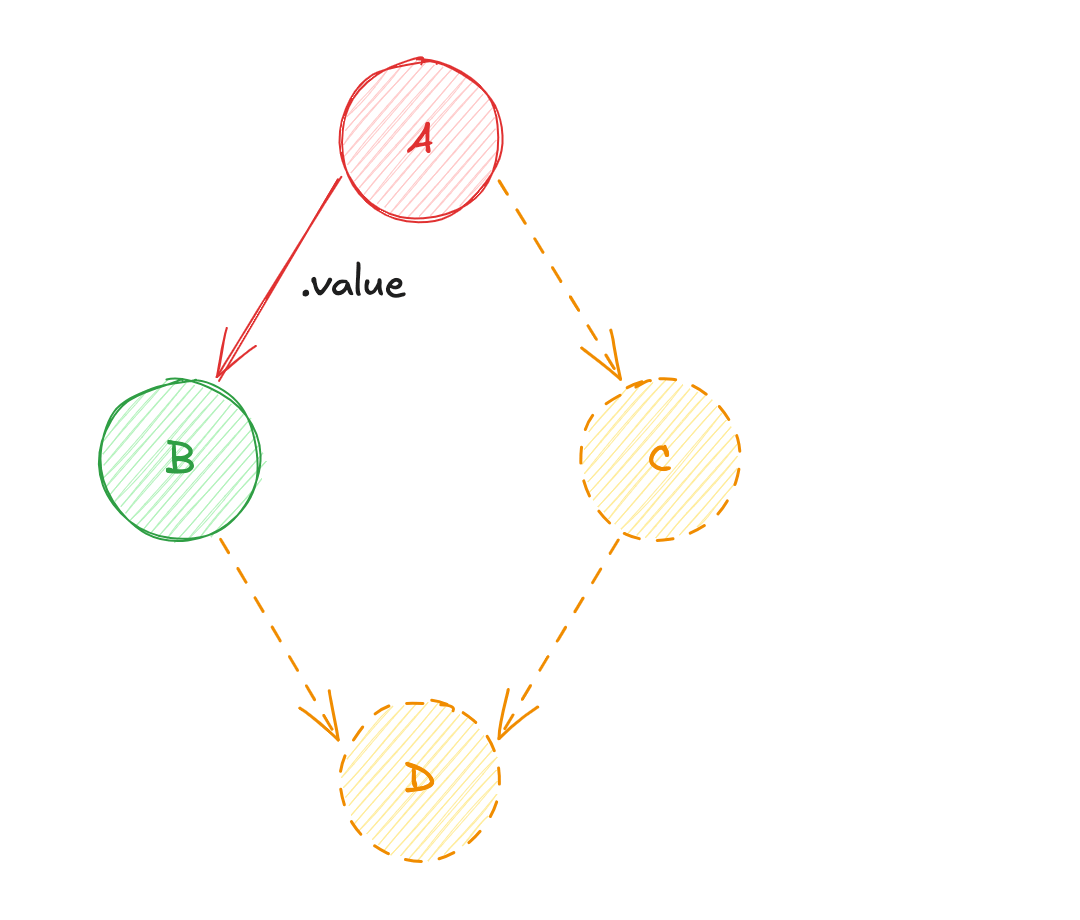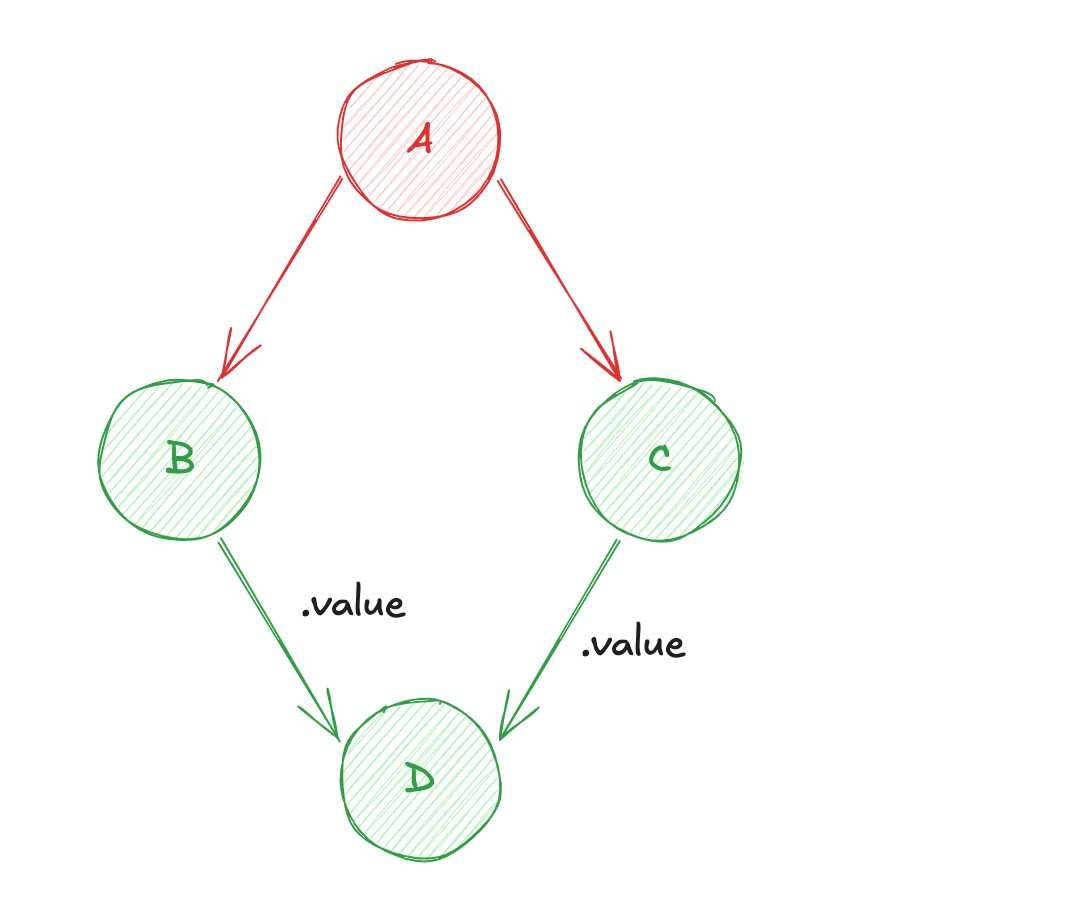
2ème Cas d'Usage : Prochaine Itération

Admettons l'état suivant,

let a = signal({ firstName: 'Jane', lastName: 'Doe' });
let e = signal('');
const b = computed(() => a.value.firstName);
const c = computed(() => `${e.value} ${e.value.lastName}`);
const d = computed(() => `${b.value} ${c.value}`);

effect(() => console.log(d.value));
e.value = 'Phoenix';

À nouveau, l'aspect "granulaire" du système "PUSH-PULL", va permettre de suivre automatiquement chaque état. Ainsi, l'état dérivé C suit dorénavant les états racines A et E. La mise à jour de la variable E va entraîner les actions suivantes :

• Changement d'état de la primitive réactive E !
• Notification du changement ciblé (E vers D en passant par C) ;
• E va diffuser sa valeur à C, et C va récupérer la valeur de A par mémoïsation (re-calcul de la valeur de C) ;
• C va diffuser sa valeur à D, et D va récupérer la valeur de B par mémoïsation (re-calcul de la valeur de D) ;

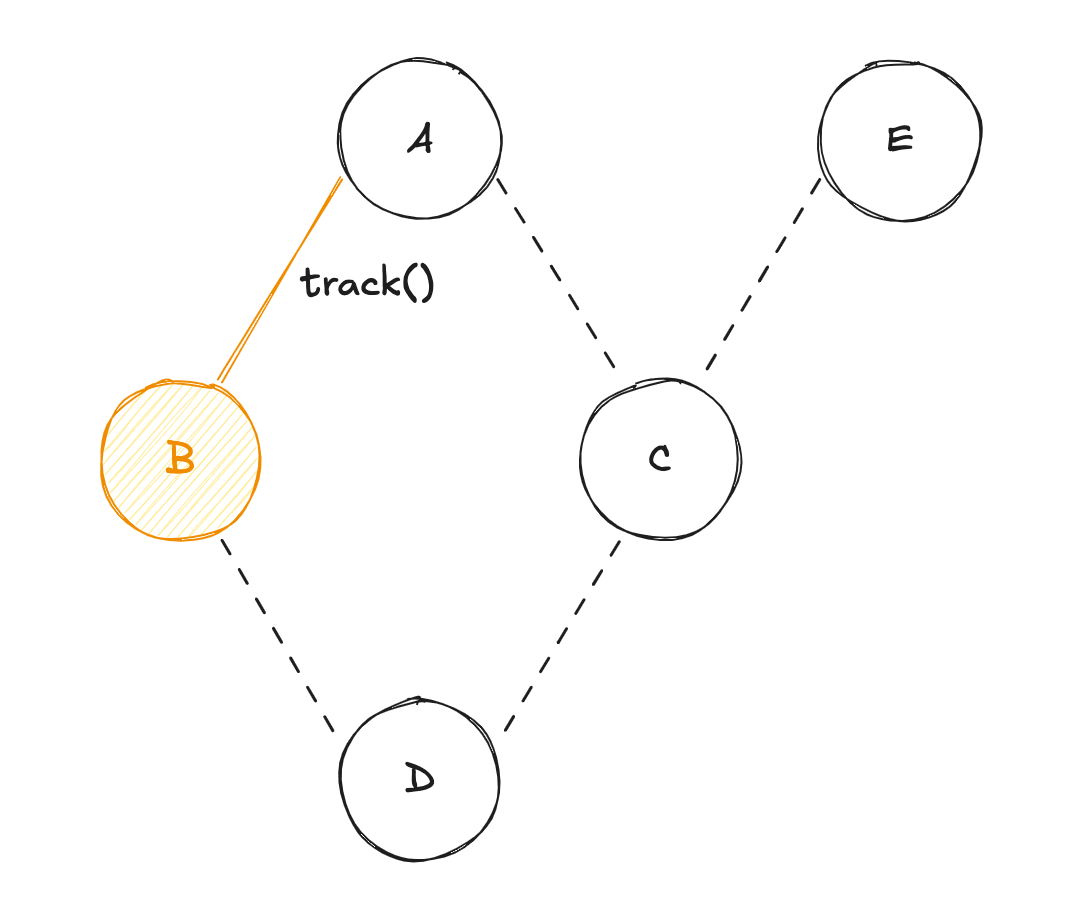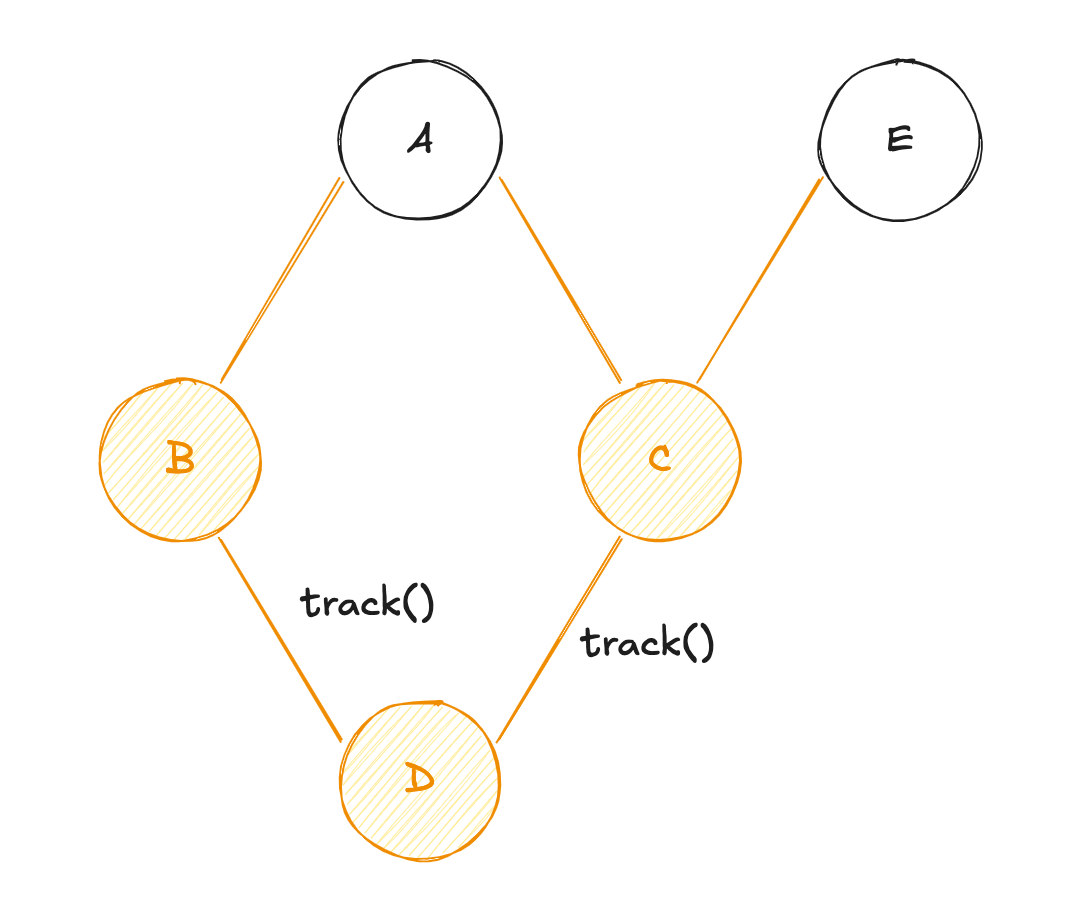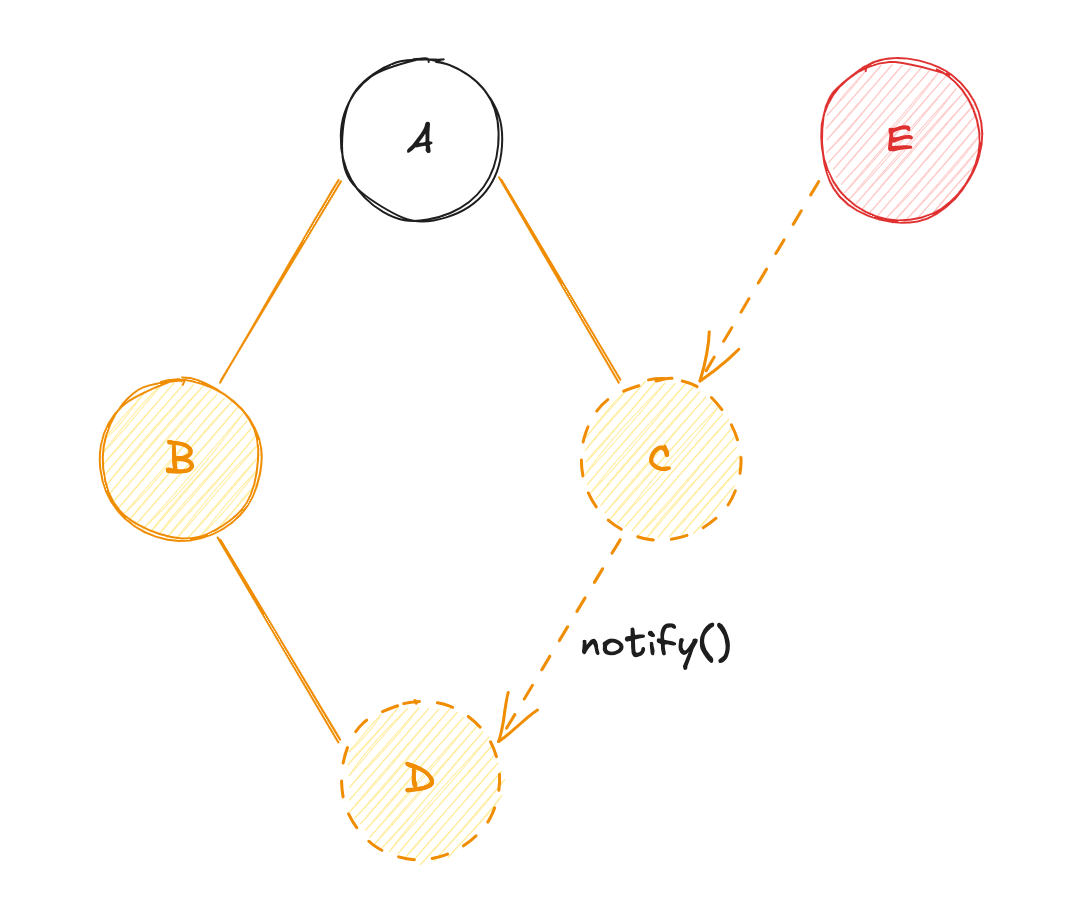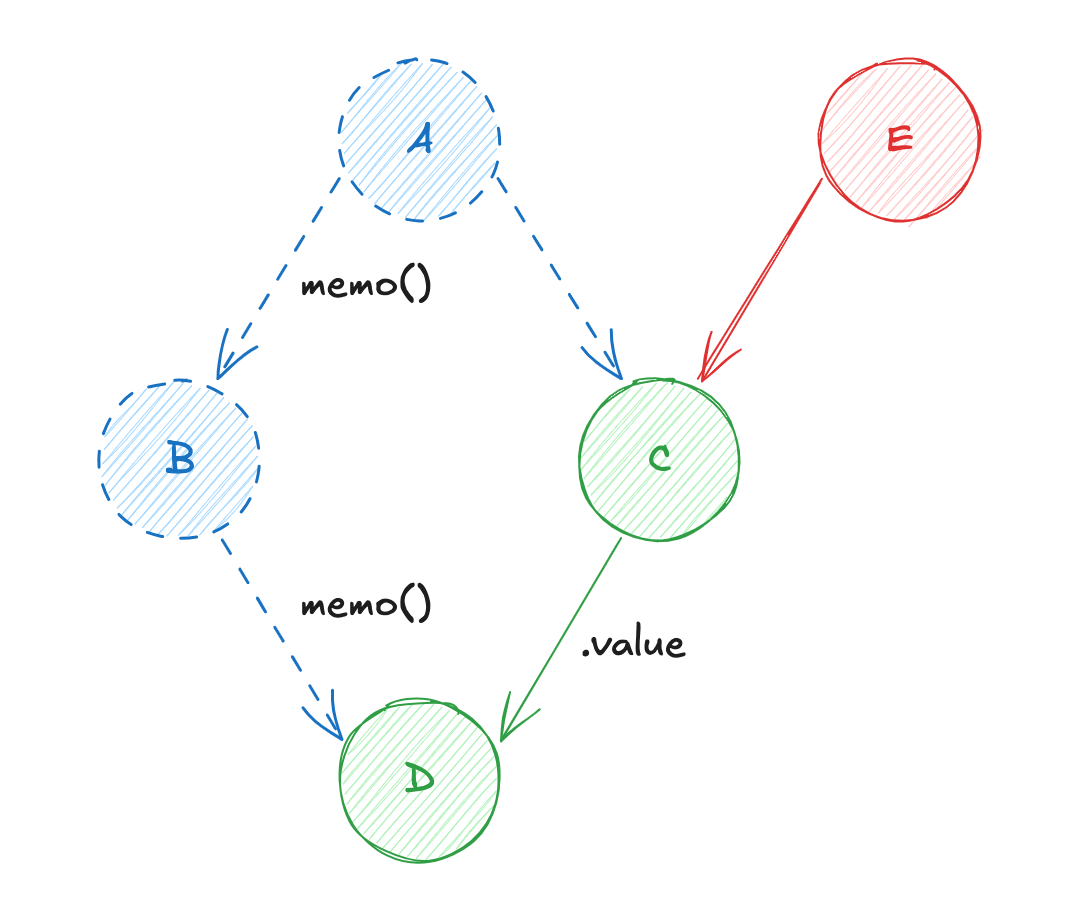
C'est cette association préalable des dépendances réactives entre elles qui rend ce modèle si performant !

En effet, en prenant un système "PULL" classique (le Virtual DOM de React, par exemple), lors de la mise à jour d'un état réactif depuis un composant, le framework va être notifié du changement (ce qui va déclencher une phase de "diffing"). Ensuite, à la demande (et de manière différée), le framework va calculer le/les changements en remontant l'arbre de dépendances réactives ; à chaque fois qu'une variable est mise à jour ! Cette "découverte" de l'état des dépendances a un coût non négligeable...

Avec un système à réactivité "granulaire" (comme les Signals), la mise à jour de variables/primitives réactives va automatiquement notifier du changement tout état dérivé qui leur est lié. Ainsi, plus besoin de (re)découvrir les dépendances associées ; la propagation de l'état est ciblée !

Conclusion(.value)

En 2024, la plupart des frameworks web ont fait le choix de revoir leur mode de fonctionnement, notamment en ce qui concerne le modèle de réactivité. Ce qui les rend globalement plus performants et compétitifs. D'autres font le choix d'être (encore) hybrides (je pense ici à Vue), ce qui les rend davantage flexibles dans bien des situations.

Finalement, quel que soit le modèle choisi, selon moi, un (bon) système réactif réside dans ces quelques règles :

1. Le système empêche les états dérivés incohérents ;
2. L'utilisation d'un état au sein du système entraîne un état dérivé réactif ;
3. Le système minimise le travail excessif ;
4. Enfin, "pour un état initial donné, quel que soit le chemin suivi par l'état, le résultat final du système sera toujours le même !"

Ce dernier point, qui peut être interprété comme un principe fondamental de la programmation déclarative ; je le vois comme le fait qu'un (bon) système réactif se doit d'être déterministe ! C'est ce "déterminisme" qui rend un modèle réactif fiable, prédictible et simple à utiliser dans des projets techniques à l'échelle, peu importe la complexité de l'algorithme.